This post will dive into various ways of thinking about rotations mathematically, and which method we think is best.
Wednesday, July 17, 2019
First, what is a rotation?
A rotation, simply put, changes the orientation of an object while maintaining its shape.
A rotation can occur either on an object or its coordinate frame. These are equal but opposite, and which is essentially the difference between picking up a Rubik’s cube and turning which side faces you (object rotation), or leaving it on the table and moving around it to change the angle in which you view it (coordinate frame rotation).
Mathematical approaches to rotations:
There are several mathematical approaches to represent rotations. Each approach has tradeoffs, and potential pitfalls around coordinate systems, signs, frame versus vector rotation and rotations that are not commutative. Let’s take a look at the pros and cons for each:
Euler angles
This is based on the principle that any rotation happening in space can be described by using three angles. There are twelve unique rotation sequences that can be generated using this approach. These sequences can be extrinsic, where the rotation axes are fixed globally, or intrinsic, where the rotation axes move with the device. You’ll rarely do computations using extrinsic Euler angles.
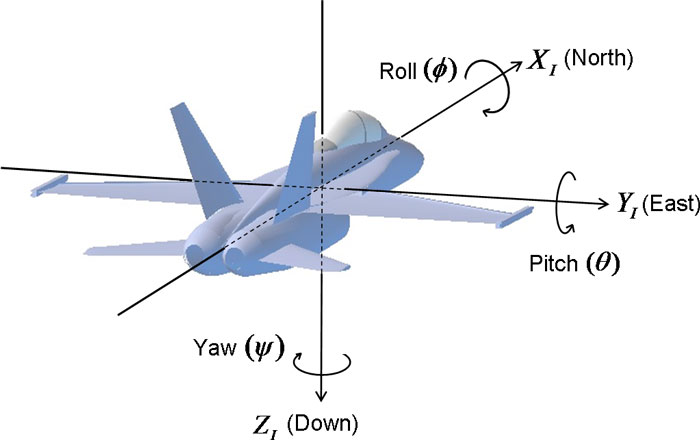
Perhaps the most common of these sequences for pitch, yaw and roll is the aerospace Euler sequence.
It’s based on an NED coordinate system (north east down), where North is X, East is Y, and Z is down. To better understand how intrinsic sequences work, consider the image above. If we wanted to follow a sequence of Z-Y’-X”, we would rotate the plane about the center of the plane/gravity (Z), then rotate the plane about the wings (Y’) based on this new position, then finally rotate about the center cylindrical body of the plane (X”).
This particular sequence of yaw, pitch, and roll angles (Z-Y’-X”) is known as a Tait-Bryan angle, but is colloquially referred to as Euler angles.
Euler angles are easier to read, making them easier for people to think through. As such, this approach is useful for conceptualizations and user input, but it’s not very useful for computation or interpolation (e.g., if you think about yaw and pitch as latitude and longitude of the earth, one degree of motion at the equator is significantly more motion than one degree of motion at the polar ice caps). One major drawback of using Euler angles is gimbal lock. This is when your middle rotation approaches π/2 (or 90 degrees). The easiest way to picture this if we go back to the Tait-Bryan angle and rotate any amount about gravity (Z), but then tilt the plane (pitch/Y’) up 90 degrees: then the plane is facing straight up. At that point, rolling about the center of the plane is the same as rotating around gravity. This “locks” you into a system with two degrees of freedom (DoF), and loses the third. This loss produces redundant equivalent rotations that make computations very messy.
Direction cosine matrices (DCM)
DCM, also referred to as Rotation Matrix, is a 3×3 matrix representation, where
w = Rv (Rotation x vector)
It’s used to transform one coordinate reference frame to another, and is equivalent to the product of the individual Euler angle rotations, just expressed as matrices. When using this method, there must be an orthogonal matrix (where R-1 = RT and Det(R) = 1), to represent a pure rotation (that doesn’t scale or skew). Gimbal lock can be avoided using DCM, but the major drawback of this method is that it can become computationally costly to make sure that your matrix maintains orthogonality after manipulations.
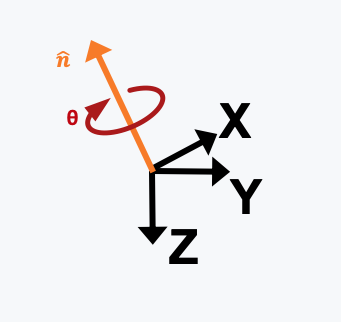
Axis-Angle
As opposed to the Euler angles which need three rotations, axis-angle representations only need one rotation; the theory posits that any rotation can be represented by a single rotation, θ, around an arbitrary axis, n. The benefit of this approach is that there are only two numbers to manipulate during calculations, as opposed to three (as with Euler angles) or nine (as with DCM). This delivers numeric stability that the Euler angle approach lacks (no need to renormalize like DCM, no gimbal lock like Euler), but its large drawback is that it’s not a very suitable method for additional computation.
Quaternions
Quaternions can be used in conjunction with or as an alternative to the other rotational approaches discussed above, and is our preferred approach for defining rotations. This representation uses a complex number with one real term and three imaginary terms:
q = w + xi + yj + zk, where w is a real term, and x, y, z, are the imaginary terms; or a vector representation of q = [w,x,y,z] = [w,a] where w is a real term and a = vector (x,y,z)
Quaternions eliminate the risk of gimbal lock and are more numerically stable than DCM: there are no redundant factors, no (costly) need to orthogonalize over manipulations and it’s easier to maintain normalization.
Normalized quaternions can express rotation of an arbitrary vector around an arbitrary angle, similar to the axis-angle approach. This makes it easier to interpret:
w is a warped version of the angle: w = cos(θ/2)
a = [x,y,z] is a scaled version of the axis:
- a = (x,y,z) = n sin(θ/2)
- n = a / | a |
In quaternion math, addition is vector addition (the sum of all parts).
Multiplication is a bit more complicated, however, and not commutative. If we define P as (p0, p) and Q as (q0, q), then P⊗Q = p0q0 – p·q + p0q + q0p + p⊗q.
Conjugate P* = (p0, -p)
In normalized (unit) quaternions, the inverse is equivalent to the conjugate: P-1=P*.
To rotate a vector (v) by quaternion q:
w = q* v q
v = q w q*
w = R v (where R is DCM 3×3 matrix) exists and can be found directly from quaternion
The above keeps in line with our earlier notation of a bolded letter defining a vector [x,y,z]
Combining of rotations is quaternion multiplication:
Q12 = Q1⊗Q2
And you can rotate vector v by quaternion Q and then back again:
w = Q*⊗v⊗Q
v = Q⊗w⊗Q*
For the purposes of our sensor fusion work, quaternions are advantageous because they support interpolation and derivatives. Interpolation is difficult with both axis-angle and Euler angle approaches; it can be done with DCM but is difficult because you’re performing operations on nine elements (3×3) instead of four (w,x,y,z). Quaternions are also typically more memory-efficient, since they only require four elements as compared with the nine of DCM.
However, quaternions can be computationally challenging if you’re performing large numbers of rotations. Since quaternion multiplication requires a lot of independent operations, it can actually become less computationally efficient than DCM. When doing a lot of rotations in a row, the matrix multiplications take fewer operations than quaternions.
Why We Recommend Quaternions for Sensor Fusion
As you can see, all four mathematical approaches have their own merits, as well as potential drawbacks around computational ease. When doing rotational mathematics for sensor fusion, we prefer quaternions. You will avoid gimbal lock, ensure numerical stability, be able to interpolate the signal, and realize gains in processing efficiency.
You might also like
More from Sensor fusion
Evaluating Spatial Audio – Part 1 – Criteria & Challenges
We here at Ceva, have spoken at length about spatial audio before, including this blog post talking about what it …
Gyro Pen Revolution: From Passive Stylus to Motion Pen
Imagine you’re a school teacher using the latest technology to engage your students. The class thrives on interactive presentations and …